Turunan Fungsi
 |
| Turunan Fungsi |
Turunan fungsi adalah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f' yang mempunyai nilai tidak beraturan.
Perbedaan Differensial dan Derivative
- Differensial
 |
| Differensial |
Ketika garis singgung menyinggung grafik f pada titik (c, f(c))

digunakan sebagai perkiraan grafik f, kuantitas x – c disebut sebagai perubahan dalam x, dan dinotasikan sebagai ∆x, seperti yang ditunjukkan oleh gambar di bawah ini.

Jika ∆x kecil, maka perubahan di y (dinotasikan dengan ∆y) dapat diperkirakan seperti berikut.

Untuk pendekatan yang seperti itu, kuantitas ∆x biasanya dinotasikan dengan dx, dan disebut diferensial x. Bentuk f ’(x)dx dinotasikan dengan dy, dan disebut sebagai diferensial y.
Definisi DiferensialMisalkan y = f(x) merupakan suatu fungsi yang dapat diturunkan pada selang buka yang memuat x. Diferensial x (dinotasikan dengan dx) adalah sebarang bilangan real tidak nol. Diferensial y (dinotasikan dengan dy) adalah
Dalam berbagai jenis penerapan, diferensial y dapat digunakan sebagai perkiraan perubahan di y. Yaitu,

Contoh 2: Membandingkan ∆y dan dy
Misalkan y = x². Tentukan dy ketika x = 1 dan dx = 0,01. Bandingkan nilai ini dengan ∆yuntuk x = 1 dan ∆x = 0,01.
Pembahasan Karena y = f(x) = x², kita memiliki f ’(x) = 2x, dan diferensial dy adalah

Sekarang, dengan menggunakan ∆x = 0,01, perubahan di y adalah

Gambar di bawah menunjukkan perbandingan dy dan ∆y secara geometris. Apabila kita mencoba nilai-nilai lain dy dan ∆y, kita akan melihat bahwa kedua nilai tersebut akan semakin dekat satu sama lain jika dx (atau ∆x) mendekati 0.

Pada Contoh 2, persamaan garis singgung grafik f(x) = x² pada x = 1 adalah 2x – 1. Untuk nilai-nilai x yang dekat dengan 1, garis ini akan dekat ke grafik f, seperti yang ditunjukkan gambar di atas dan tabel berikut.

Jadi,turunan adalah hasil pembagian antara 2 buah diferensial.Sebagai contoh,Jika kita mengatakan bahwa "turunan dari  adalah
adalah  ", maka pernyataan itu adalah BENAR, karena
", maka pernyataan itu adalah BENAR, karena  . Tapi, akan SALAH jika turunan disamakan dengan diferensial. Jika kita mengatakan bahwa "diferensial dari
. Tapi, akan SALAH jika turunan disamakan dengan diferensial. Jika kita mengatakan bahwa "diferensial dari  adalah
adalah  ", maka pernyataan itu adalah SALAH. Kalau ingin betulnya, harus seperti ini: "diferensial dari
", maka pernyataan itu adalah SALAH. Kalau ingin betulnya, harus seperti ini: "diferensial dari  adalah
adalah  dikalikan dengan diferensial x" atau dapat ditulis begini:
dikalikan dengan diferensial x" atau dapat ditulis begini: 
Lalu, kenapa dinamakan diferensial?Ingat-ingat kembali rumus turunan: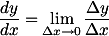
Diferensial adalah selisih variabel (Ingat "difference" dalam bahasa inggris artinya "beda", bukan?).. Sekadar mengingatkan, di rumus di atas, maka x adalah variabel bebas sedangkan y adalah variabel terikat.. Sebenarnya, bisa saja rumusnya begini: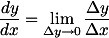
Di atas maka y adalah variabel bebas sedangkan nilai x terikat terhadap variabel y.Jika  , maka
, maka 
Proses penurunan sebuah fungsi disebut proses pendiferensian atau diferensiasi,merupakan penentuan limit suatu kuosien diferensiasi dalam pertambahan variable bebas yang sangat kecil atau mendekati nol.
Hasil dari proses pendiferensiasi disebut turunan atau derivative.
Dengan demikian : Jika y = f (x)
Maka kuosien diferensinya : ( kd) :
Dan turunan fungsinya :
Contoh
Persamaan y = 4x2 – x
Kuosien difrensiasi : = 8 x + 3 x -1
= 8x +3(0) -1
= 8x – 1
Jadi turunan (derivatif) dari fungsi y = 4 x2 – x adalah: 8 x – 1
Hasil dari proses pendiferensiasi disebut turunan atau derivative.
Dengan demikian : Jika y = f (x)
Maka kuosien diferensinya : ( kd) :
Dan turunan fungsinya :
Contoh
Persamaan y = 4x2 – x
Kuosien difrensiasi : = 8 x + 3 x -1
= 8x +3(0) -1
= 8x – 1
Jadi turunan (derivatif) dari fungsi y = 4 x2 – x adalah: 8 x – 1
Kaidah-kaidah diferensiasi
1.Diferensiasi konstanta
Jika y = k, dimana k adalah konstanta, maka dy/dx = 0
contoh : y = 5 à dy/dx = 0
2.Diferensiasi fungsi pangkat
Jika y = xn, dimana n adalah konstanta, maka dy/dx = nxn-1
contoh : y=x3àdy/dx=3x3-1=3x2
3. Diferensiasi perkalian konstanta dengan fungsi
Jika y = kv, dimana v = h(x),
à dy/dx = k dv/dx
contoh : y = 5x3 à dy/dx = 5(3x2) = 15x2
4. Diferensiasi pembagian konstanta dengan fungsi
jika y = k/v, dimana v=h(x), maka :
5. Diferensiasi penjumlahan (pengurangan) fungsi
jika y = u + v, dimana u = g(x) dan v = h(x)
maka dy/dx = du/dx + dv/dx
contoh : y = 4x2 + x3 à u = 4x2 du/dx = 8x
à v = x3 dv/dx = 3x2
dy/dx =du/dx + dv/dx = 8x + 3x2
6. Diferensiasi perkalian fungsi
Jika y = uv, dimana u = g(x) dan v = h(x)
7. Diferensiasi pembagian fungsi
Jika y = u/v. dimana u = g(x) dan v = h(x)
Rumus turunan dasar
Umum
Eksponen dan bilangan natural
Logaritma dan bilangan natural
Trigonometri
- Invers
- Hiperbolik
Turunan (derivatif) membahas tingkat perubahan suatu fungsi sehubungan dengan perubahan kecil dalam variabel bebas fungsi yang bersangkutan.
Langkah-langkah untuk mencari turunan pertama ialah:
(1) Tentukan kenaikan x dan y untuk memperoleh
y + f(x +
(2) Kurangkan y = f(x) dari hasil butir (1) itu untuk memperoleh
= f(x + f(x)
(3) Bagi rumusan butir (2) dengan untuk memperoleh hasil bagi diferensiasi
=
(4) Tentukan limit dari hasil bagi diferensiasi itu ketika 0, sehingga diperoleh turunan pertama.
Turunan Penjumlahan dan Pengurangan Fungsi
Penjumlahan Fungsi
Contoh
Jika f(x) = 5x + 4 dan g(x) = 6x² + 2x + 3
(f + g)(x) = f(x) + g(x) =
5x + 4 + 6x² + 2x + 3 = 6x² + 5x + 2x + 4 + 3
= 6x² + 7x + 7.
Pengurangan Fungsi
Contoh
Jika f(x) = 5x + 4 dan g(x) = 6x² + 2x + 3, maka
(f - g)(x) = f(x) - g(x)
= 5x + 4 - (6x² + 2x + 3)
= -6x² + 5x - 2x + 4 - 3
= -6x² + 3x + 1.
Penjumlahan Fungsi
Contoh
Jika f(x) = 5x + 4 dan g(x) = 6x² + 2x + 3
(f + g)(x) = f(x) + g(x) =
5x + 4 + 6x² + 2x + 3 = 6x² + 5x + 2x + 4 + 3
= 6x² + 7x + 7.
Pengurangan Fungsi
Contoh
Jika f(x) = 5x + 4 dan g(x) = 6x² + 2x + 3, maka
(f - g)(x) = f(x) - g(x)
= 5x + 4 - (6x² + 2x + 3)
= -6x² + 5x - 2x + 4 - 3
= -6x² + 3x + 1.
Turunan Penjumlahan dan Pengurangan Fungsi
Fungsi Perkalian f'(x)=u(x).v'(x)+u'(x).v(x)
Contoh
tentukan Y' dari
Y= (2x²+x)(4x+1)
Jawab:
Fungsi Pembagian
Jika kita memiliki persamaan y= f(x)/g(x), dengan f(x), g(x) memiliki satu variabel linear; atau dapat kita tulis y=(ax + b)/(cx+d), maka untuk mendapatkan nilai turunannya adalah kita biasa memisalkan ax+b=u dan cx+d=v, sehingga kita mendapatkan nilai turunan sebagai berikut
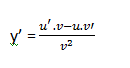
Fungsi Trigonometri
Fungsi Perkalian f'(x)=u(x).v'(x)+u'(x).v(x)
Contoh
tentukan Y' dari
Y= (2x²+x)(4x+1)
Jawab:
U=2x²+x
U’=4x+1
V=4x+1
V’=4
Y’=U’V+UV’
Y’=(4X+1)(4x+1)+(2x²+x)(4)
Y’=(16x²+4x+4x+1)+(8x²+4x)
Y’=24x²+12x+1
Fungsi Pembagian
Jika kita memiliki persamaan y= f(x)/g(x), dengan f(x), g(x) memiliki satu variabel linear; atau dapat kita tulis y=(ax + b)/(cx+d), maka untuk mendapatkan nilai turunannya adalah kita biasa memisalkan ax+b=u dan cx+d=v, sehingga kita mendapatkan nilai turunan sebagai berikut
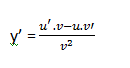
Jawab:
Diferensiasi fungsi trigonometri atau turunan fungsi trigonometri adalah proses matematis untuk menemukanturunan suatu fungsi trigonometri atau tingkat perubahan terkait dengan suatu variabelnya. Fungsi trigonometri yang umum digunakan adalah sin(x), cos(x) dan tan(x). Contohnya, turunan "f(x) = sin(x)" dituliskan "f ′(a) = cos(a)". "f ′(a)" adalah tingkat perubahan sin(x) di titik "a". Semua turunan fungsi trigonometri lingkaran dapat ditemukan dengan menggunakan turunan sin(x) dan cos(x). Kaidah hasil bagi lalu digunakan untuk menemukan turunannya. Sementara itu, pencarian turunan fungsi trigonometri invers membutuhkan diferensiasi inplisit dan turunan fungsi trigonometri biasa.
Turunan fungsi trigonometri
Turunan fungsi trigonometri
- contoh-contoh soal:
Soal No. 1
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 3x4 + 2x2 − 5x
b) f(x) = 2x3 + 7xPembahasan
Rumus turunan fungsi aljabar bentuk axn Sehingga:
Sehingga:
a) f(x) = 3x4 + 2x2 − 5x
f ‘(x) = 4⋅3x4− 1 + 2⋅2x2−1 − 5x1-1
f ‘(x) = 12x3 + 4x1 − 5x0
f ‘(x) = 12x3 + 4x − 5b) f(x) = 2x3 + 7x
f ‘(x) = 6x2 + 7Soal No. 2
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 10x
b) f(x) = 8
c) f(x) = 12Pembahasan
a) f(x) = 10x
f(x) = 10x1
f ‘(x) = 10x1−1
f ‘(x) = 10x0
f ‘(x) = 10 b) f(x) = 8
b) f(x) = 8
f(x) = 8x0
f ‘(x) = 0⋅ 8x0−1
f ‘(x) = 0 c) f(x) = 12
c) f(x) = 12
f ‘(x) = 0Soal No. 3
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x2 + 4x)
b) f(x) = (2x + 3)(5x + 4)Pembahasan
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x2 + 4x)
f(x) = 10x2 + 20x
f ‘ (x) = 20x + 20b) f(x) = (2x + 3)(5x + 4)Urai terlebih dahulu hingga menjadi
f (x) = 10x2 + 8x + 15x + 12
f (x) = 10x2 + 13x + 12
Sehingga
f ‘ (x) = 20x + 13 - Semoga Bermanfaat Temen-TemenTerimakasih
DIFER












































Komentar
Posting Komentar