Hubungan (Relasi) & Fungsi (Function)
Hallo kakak bertemu lagi dengan sayaa di blog ini hihi :D
Kali ini saya akan membahas materi tentang "Hubungan (Relasi) & Fungsi (Function)".
Tapi...sebelum itu saya akan membahas sedikit materi tentang Bilangan Real dan tambahan materi yaitu tentang Pasangan Berurutan(Ordered Pairs) dan Kuadran (Hyperplanes).
A. Garis dan Bilangan Riil
Setiap garis lurus menyatakan :
3. Setiap bilangan riil merupakan titik di atas garis lurus(the real lines).
Setiap garis lurus menyatakan :
- Himpunan semua bilangan rill (dengan notasi R) karena garis lurus memuat semua bilangan riil yang terdiri dari :
- Bilangan Rasional(bulat dan pecahan)
- Bilangan Irrasional
3. Setiap bilangan riil merupakan titik di atas garis lurus(the real lines).
B. Pasangan Beruntun (Ordered Pairs)
Pasangan Beruntun (Ordered Pairs)adalah pengaitan dua buah anggota himpunan dengan memperhatikan urutan. Beda halnya pada himpunan, pasangan dua anggota pada himpunan tidak memperhatikan urutan, misal A = (1, 2) dan B = (2, 1), maka A = B, tapi pada pasangan terurut tidak berlaku. Misalkan pasangan beruntun terdiri atas dua buah elemen yaitu a dan b dengan notasi (a, b), ini artinya bahwa pasangan terurut dua anggota suatu himpunan dengan urutan pertama a dan urutan kedua b. Oleh karena itu, jika a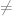 b maka (a, b)
b maka (a, b) 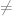 (b,a). Secara matematis, pasangan beruntun terdiri dari:
(b,a). Secara matematis, pasangan beruntun terdiri dari:
Pasangan Beruntun (Ordered Pairs)adalah pengaitan dua buah anggota himpunan dengan memperhatikan urutan. Beda halnya pada himpunan, pasangan dua anggota pada himpunan tidak memperhatikan urutan, misal A = (1, 2) dan B = (2, 1), maka A = B, tapi pada pasangan terurut tidak berlaku. Misalkan pasangan beruntun terdiri atas dua buah elemen yaitu a dan b dengan notasi (a, b), ini artinya bahwa pasangan terurut dua anggota suatu himpunan dengan urutan pertama a dan urutan kedua b. Oleh karena itu, jika a
- Pasangan tidak berurutan(Unordered Pairs) merupakan dua set yang sama karena mempunyai elemen yang sama tetapi tidak memperdulikan kesamaan urutan atau order elemen masing-masing set. Contoh : Menyebut anggota dalam suatu pertandinagan tanpa urutan. Misal Dandi dan Dhimas adalah anggota sepakbola. Jadi apabila menyebutkan Dhimas dan Dandi adalah anggota sepakbola tidak masalah.
- Pasangan berurutan(Ordered Pairs) meupakan dua set yang tidak sama (walaupun memiliki elemen yang sama), karena urutan atau order elemen masing-masing set tidak sama, kecuali apabila a = b. Contoh : Untuk set dengan elemen ordered pair, dimana elemen pertama untuk umur dan elemen kedua untuk berat, tentu akan beda antara set {45, 60} dan {60, 45}.
C. Ordered Pairs Pada Kuadran
4 (empat) kuadran (quadrant) I, II, III, IV, atau disebut the xy plane, dimana :
4 (empat) kuadran (quadrant) I, II, III, IV, atau disebut the xy plane, dimana :
- Kudran I dimana terdapat jumlah tak terbatas dari ordered pairs dengan urutan +x (angka x positif) dan +y (angka y positif).
- Kuadran II dimana terdapat jumlah tak terbatas dari ordered pairs dengan urutan −x (angka x negatif) dan +y.
- Kuadran III dimana terdapat jumlah tak terbatas dari ordered pairs dengan urutan −x dan −y (angka y negatif).
- Kuadran IV dimana terdapat jumlah tak terbatas dari ordered pairs dengan urutan +x dan −y
Titik-titik kombinasi dari titik x pada sumbu/garis x dan titik y pada sumbu/garis y secara berurutan, disebut the xy ordered pairs. Misal, titik kombinasi atau the xy ordered pair (6,8) berbeda dengan the xy ordered pair (8,6).
baiklah setelah membahas yang diatas,sekarang saya akan langsung membahas materi ini let's go:
HUBUNGAN DAN FUNGSI
 |
| Hubungan&Fungsi |
A. Pengertian Hubungan(Relasi)
Hubungan(Relasi) dapat diartikan sebagai hubungan. Hubungan yang dimaksud di sini adalah hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Kedua jenis daerah akan dijelaskan kemudian. Sedangkan fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya. Perbedaan antara relasi dan fungsi terletak pada cara memasangkan anggota himpunan ke daerah asalnya.
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.
Kesimpulannya, setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi. Penjelasan mengenai relasi dan fungsi dapat dilihat pada gambar diatas.
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah ini:
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah ini:
Untuk mengerjakan soal Relasi terdapat tiga metode yaitu diagram panah, diagram cartesius, dan himpunan pasangan berurutan.
1. Diagram Panah
Himpunan E sebagai domain (daerah asal) diletakkan di sebelah kiri, dan himpunan F sebagai kodomain (kodomain) diletakkan di sebelah kanannya. Relasi antara himpunan E dan F ditunjukkan dengan arah panah. Seperti gambar di bawah ini
Himpunan E sebagai domain (daerah asal) diletakkan di sebelah kiri, dan himpunan F sebagai kodomain (kodomain) diletakkan di sebelah kanannya. Relasi antara himpunan E dan F ditunjukkan dengan arah panah. Seperti gambar di bawah ini
2. Himpunan Pasangan Berurutan
Jika x elemen E dan y elemen F, maka relasi dari E ke F dapat dinyatakan dengan pasangan berurutan (x, y). Dari diagram panah di atas dapat dituliskan himpunan pasangan berurutannya sebagai berikut: {(1, 2), (1, 4), (1, 6), (2, 4), (2, 6), (3, 4), (3, 6), (4, 6), (5, 6)}.
Jika x elemen E dan y elemen F, maka relasi dari E ke F dapat dinyatakan dengan pasangan berurutan (x, y). Dari diagram panah di atas dapat dituliskan himpunan pasangan berurutannya sebagai berikut: {(1, 2), (1, 4), (1, 6), (2, 4), (2, 6), (3, 4), (3, 6), (4, 6), (5, 6)}.
3. Diagram Cartesius
Pada koordinat cartesius daerah asal (domain) diletakkan pada sumbu X (sumbu mendatar) dan daerah kawan (kodomain) diletakkan pada sumbu Y (sumbu tegak). Sedangkan daerah hasilnya merupakan titik (noktah) koordinat pada diagram cartesius. Dari relasi di atas, dapat ditunjukkan diagram cartesiusnya seperti di bawah ini:
Pada koordinat cartesius daerah asal (domain) diletakkan pada sumbu X (sumbu mendatar) dan daerah kawan (kodomain) diletakkan pada sumbu Y (sumbu tegak). Sedangkan daerah hasilnya merupakan titik (noktah) koordinat pada diagram cartesius. Dari relasi di atas, dapat ditunjukkan diagram cartesiusnya seperti di bawah ini:
Setiap titik atau ordered pair pada the xy plane atau the Cartesian product menunjukkan terjadi hubungan (relation) :
"Antara setiap bilangan riil atau titik pada garis atau variabel x dengan bilangan riil atau titik pada garis atau variabel y, jadi, terdapat set (x, y) atau ordered pair atau titik pada the xy plane sebagai dari hasil hubungan (asosiasi) atas dasar suatu aturan dari setiap bilangan atau angka x dengan bilangan atau angka y."
Misal pada Diagram 1. di atas :
- Titik (x, y) = (1,2) di kuadran I, menunjukkan bahwa atas dasar suatu aturan, maka untuk x =1 mempunyai hubungan dengan y = 2.
- Juga titik (x, y) = (−2, 1) di kuadran II menunjukkan hubungan x = − 2 dengan y = 1 berdasarkan suatu aturan
- Hubungan bukan bersifat satu-satu atau kausal. Dengan hubungan ini, maka atas dasar suatu aturan satu bilangan dari set x akan berhubungan atau menghasilkan lebih dari satu bilangan dari set y. Jadi hubungan tidak bersifat kausal atau satu-satu (one-to-one relation). Suatu aturan dimaksud disebut sebagai hubungan (relation atau a multivalued function).
- Hubungan merupakan fungsi bila hubungan bersifat satu-satu atau kausal (one-to-one relation or correspondence, atau unique relation). Dengan hubungan ini, maka atas dasar suatu aturan satu bilangan dari set x akan berhubungan atau menghasilkan hanya satu bilangan dari set y. Jadi hubungan bersifat kausal atau satu-satu (one-to-one relation). Suatu aturan dimaksud disebut sebagai fungsi (function) atau a single-valued function
B.Pengertian Fungsi(Function)
Fungsi atau yang sering disebut juga dengan pemetaan masih termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.
Simbol fungsi yang memetakan himpunan A ke B adalah
![Rendered by QuickLaTeX.com \[ f: \; A \rightarrow B\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6fcd2503c617afc66fb662d8ac5083a0_l3.png) Contoh pemasalahan pada fungsi:
Contoh pemasalahan pada fungsi:
Diketahui himpunan A dan B diberikan seperti di bawah.
![Rendered by QuickLaTeX.com \[ A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-643bf49e5f45e692e5a4ffca0538aaeb_l3.png)
![Rendered by QuickLaTeX.com \[ B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-440212b7cc191c741c4a0aba87d632a9_l3.png) Didefinisikan fungsi
Didefinisikan fungsi  dengan f(x) = x + 5.
dengan f(x) = x + 5.
Tentukan hasil pemetaan dari oleh fungsi
oleh fungsi 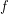 ,
,  ,
, 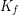 , dan
, dan 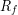 !
!
Pembahasan:
Peta dari oleh fungsi f yaitu y = f(x):
oleh fungsi f yaitu y = f(x):
![Rendered by QuickLaTeX.com \[ f(0) = 0 + 5 = 5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c4ebb9c99c38503f006f99eb66e3b0db_l3.png)
![Rendered by QuickLaTeX.com \[ f(1) = 1 + 5 = 6 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d2118a577e3819445aa95e455f670d67_l3.png)
![Rendered by QuickLaTeX.com \[ f(2) = 2 + 5 = 7 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-03b90256b4833280c8bba9ebac02eafe_l3.png)
![Rendered by QuickLaTeX.com \[ f(3) = 3 + 5 = 8 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-9c26831a27c317d4dcb853763c6221b9_l3.png)
![Rendered by QuickLaTeX.com \[ f(4) = 4 + 5 = 9 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-eee345654dad9700db41710aaf317543_l3.png)
 = Daerah Asal
= Daerah Asal
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{ 0, 1, 2, 3, 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0e91b7c13ff17e363486f70d260275d6_l3.png)
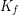 = Daerah Kawan
= Daerah Kawan
![Rendered by QuickLaTeX.com \[ K_{f} = B = \left \{ 0, 1, 2, ..., 10 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ed9c47be5a6fc3133226b166bf608a00_l3.png)
Daerah Hasil =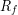
![Rendered by QuickLaTeX.com \[ D_{f} = A = \left \{5, 6, 7, 8, 9 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-31e10c571e8cd9ebd151c45afe542a75_l3.png)
Simbol fungsi yang memetakan himpunan A ke B adalah
Diketahui himpunan A dan B diberikan seperti di bawah.
Tentukan hasil pemetaan dari
Pembahasan:
Peta dari
Daerah Hasil =
Sifat-sifat fungsi:
Fungsi injektif
Fungsi injektif
Fungsi injektif
bukan fungsi injektif

Fungsi surjektif

Bukan fungsi surjektif

Korespondensi satu-satu

Bukan korespodensi satu-satu
Jenis-jenis Fungsi
Berdasarkan letak variabel bebas (independent variables)
terdapat 2 jenis fungsi sebagai berikut:
Fungsi eksplisit (explicit function) adalah fungsi dimana (variabel bebas) independent variables berada di sebelah kanan, karena itu independent variables juga disebut right hand variables.Misal :
Fungsi implisit (implicit function) adalah fungsi dimana independent variables bersama-sama dependent variable berada di sebelah kiri, sedangkan di kanan angka 0. Misal :
Mungkin hanya itu dulu materi yang dapat saya sampaikan pada kakak-kakak sampai bertemu lagi lain waktu see you :)
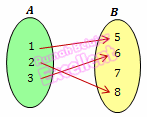
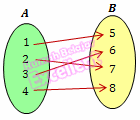
1. Fungsi injektif (satu-satu)
Jika fungsi f : A → B, setiap b ∈ B hanya mempunyai satu kawan saja di A, maka fungsi itu disebut fungsi satu-satu atau injektif.
Fungsi injektif

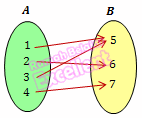
Fungsi injektif

Fungsi injektif

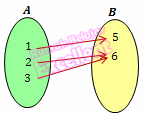
bukan fungsi injektif
2. Fungsi surjektif (onto)
Pada fungsi f : A → B, setiap b ∈ B mempunyai kawan di A, maka f disebut fungsi surjektif atau onto.
Fungsi surjektif

Bukan fungsi surjektif
3. Fungsi bijektif (korespondensi satu-satu)
Suatu fungsi yang bersifat injektif sekaligus surjektif disebut fungsi bijektif atau korespondensi satu-satu.
Korespondensi satu-satu

Bukan korespodensi satu-satu
Jenis-jenis Fungsi
terdapat 2 jenis fungsi sebagai berikut:
1. Fungsi eksplisit (explicit function)
Fungsi eksplisit (explicit function) adalah fungsi dimana (variabel bebas) independent variables berada di sebelah kanan, karena itu independent variables juga disebut right hand variables.Misal :
Fungsi : y = f(x)
Bentuk fungsi explicit : y = x2; y = a + bx; y = 3 x
2. Fungsi implicit (implicit function)
Fungsi implisit (implicit function) adalah fungsi dimana independent variables bersama-sama dependent variable berada di sebelah kiri, sedangkan di kanan angka 0. Misal :
Fungsi : g(y,x) = 0
Bentuk fungsi implicit : ax + b – y = 0; x2 + y2 = 0;
ey + y – x + ln x = 0; y mx b = 0
Selain itu terdapat beberapa jenis fungsi lainnya seperti dibawah ini:
1.FUNGSI ALJABAR
yaitu fungsi yang menggunakan operasi-operasi penjumlahan,pengurangan,perkalian,pembagian, dan penarikan akar.
yaitu fungsi yang menggunakan operasi-operasi penjumlahan,pengurangan,perkalian,pembagian, dan penarikan akar.
Contoh:
a.Fungsi irasional
yaitu fungsi yang variable bebasnya terdapat dibawah tanda akar. Misal f(x)=√x , g(x)= √x+1+3
yaitu fungsi yang variable bebasnya terdapat dibawah tanda akar. Misal f(x)=√x , g(x)= √x+1+3
b.Fungsi Rasional
yaitu fungsi yang variable bebasnya berpangkat bilangan bulat. Fungsi rasional meliputi fungsi:
yaitu fungsi yang variable bebasnya berpangkat bilangan bulat. Fungsi rasional meliputi fungsi:
- Fungsi polinom (suku banyak) memiliki bentuk
f(x)=anxn + an-1xn-1 +….+ a2x2 + a1x + a0,
dengan an , an-1 , …,a2 , a1 , a0
adalah bilangan real an ≠ 0, a0=konstanta dan n bilangan bulat
Fungsi polinom berderajat n misalkan, f(x)=2x3+4x2+6x-5
- Fungsin kubik, yaitu fungsi yang berpangkat 3. Misalkan
F(x)=x3 adalah fungsi kubik yang paling sederhana.
- Fungsi kuadrat, suatu fungsi yang berbentuk f(x)=ax2+bx+c,
Dengan a,b,c konstanta dan a≠o. Dimana grafiknya berbetuk
Parabola,domain fungsi ini adalah Df=R.
- Fungsi linear,suatu fungsi yang ditentukan oleh f(x)=ax+b,
Dengan a dan b konstanta dan a≠0. Kurva fungsi linear adalah
Garis y=ax+b yang selalu melalui titik (0,b) dan (a/b,0).
Garis y=ax+b yang selalu melalui titik (0,b) dan (a/b,0).
- Fungsi pangkat, dinyatakan dengan y=f(x)=xn, dengan n
Bilangan asli. Jika n=2→grafiknya berbentuk parabola
n=3→grafiknya berbebtuk parabola kubik
n=4→grafiknya parabola kuadrat
bentuk umum dari fungsi pangkat:y=f(x)=xn, y=f(x)=axn,
2. FUNGSI TRANSENDEN
yaitu fungsi yang bukan merupakan fungsi aljabar.
yaitu fungsi yang bukan merupakan fungsi aljabar.
Contoh:
a.Fungsi eksponen
fungsi yang variable bebasnya menjadi pangakat dari suatu
fungsi yang variable bebasnya menjadi pangakat dari suatu
bilangan . Bentuk umum y=f(x)=ax, dengan a≠0,a≠1, dan a Є R.
b. Fungsi logaritma
dengan bilangan pokok a>0 dan a≠1 adalah invers dari fungsi
dengan bilangan pokok a>0 dan a≠1 adalah invers dari fungsi
eksponen
dengan bilangan pokok a. Fungsi eksponen y=g(x)=ax, inversnya adalah fungsi
logaritma y=f(x)=alogx ; a>0 , a≠1, x>0.
c. Fungsi trigonometri
yaitu fungsi yang meliputi f9x)=sin x , f(x)=cos x ,f(x)=tan x
yaitu fungsi yang meliputi f9x)=sin x , f(x)=cos x ,f(x)=tan x
dimana x menyatakan besar suatu sudut (radian atau drajat).
3.FUNGSI KHUSUS
Contoh
a. Fungsi Konstan
Fungsi konstan adalah fungsi f yang dinyatakan dalam
Fungsi konstan adalah fungsi f yang dinyatakan dalam
rumus f(x) = c, dengan c suatu konstanta. Fungsi konstatn f memasangkan setiap
bilangan real dengan konstanta c.
b. Fungsi identitas
Fungsi I:A─>A yang ditentukan oleh I(x) disebut fungsi identitas
Fungsi I:A─>A yang ditentukan oleh I(x) disebut fungsi identitas
pada A.Fungsi I memasangkan setiap elemen daerah asal dengan dirinya sendiri.
contoh: garis y=x yang melalui titik pangkal O(o,o)
c. Fungsi modulus
fungsi f:x─>│x│ atau f(x) yang ditentukan oleh:
fungsi f:x─>│x│ atau f(x) yang ditentukan oleh:
f(x)=│x│= x,jika x ≥ 0
-x,jika x <0
Contoh: modulus y =│x│
d. Fungsi parameter
fungsi dengan parameter diantaranya adalah x=at+b,
fungsi dengan parameter diantaranya adalah x=at+b,
y=2t2 +c, dengan t adalah parameter yang menetapkan fungsi itu.
4. FUNGSI GENAP dan GANJIL
a. Fungsi genap
jika f(-x)=f(x), maka grafik tersebut simetri terhadap sumbu y .
jika f(-x)=f(x), maka grafik tersebut simetri terhadap sumbu y .
Fungsi yang demikian disebut fungsi genap.
b. Fungsi ganjil
jika f(-x)=f(-x), maka grafik tersebut simetri terhadap titik asal
jika f(-x)=f(-x), maka grafik tersebut simetri terhadap titik asal
O(0,0). Fungsi yang demikian disebut fungsi ganjil.
c. Bukan fungsi genap dan bukan fungsi ganjil
jika f(-x)≠f(x) dan f(-x)≠f(-x), maka
jika f(-x)≠f(x) dan f(-x)≠f(-x), maka
grafiknya tidak simetri terhadap titik asal.
5. FUNGSI PERIODIK
fungsi f dengan domain R dikatakan fungsi periodik apabila
fungsi f dengan domain R dikatakan fungsi periodik apabila
Terdapat bilangan k≠0, sehinga f (x+k)=f(x), dengan x Є R. Bilangan positif k terkecil
Yang memenuhi f(x+k)=f(x) disebut periode dasar fungsi itu.Mungkin hanya itu dulu materi yang dapat saya sampaikan pada kakak-kakak sampai bertemu lagi lain waktu see you :)
SEMOGA BERMANFAAT










Komentar
Posting Komentar