Materi Sistem Bilangan Real & Himpunan

 Sistem Bilangan Real & Himpunan

Sistem Bilangan Real & Himpunan

A. Sistem Bilangan Real

        Sebelum kita mempelajari kalkulus sebaiknya kita perlu memahami bahasan tentang system

bilangan real,seperti gambar di bawah ini.

Sistem Bilangan Real

Bilangan Real adalah bilangan yang terdiri dari range nilai (- tak hingga,...,-1,0,1,..., tak hingga) artinya semua bilangan yang ada pada rangetersebut merupakan bilangan real. 

Contoh deretan bilangan real adalah 

Bilangan Real terbagi menjadi dua yaitu :

1. Bilangan Rasional

   

Bilangan Rasional

   

Bilangan rasional adalah bilangan yang dapat dinyatakan sebagai a/b di mana a, b bilangan bulat dan b tidak sama dengan 0. di mana batasan dari bilangan rasional adalah mulai dari selanga (-∞, ∞).

Bilangan bisa dikatakan dapat dibagi menjadi 2 sekup besar yaitu bilangan rasional dan bilangan irasional. Bila kita mengatakan bilangan rasional berarti di dalamnya sudah mencakup bilangan: bilangan bulat, bilangan asli, bilangan cacah, bilangan prima dan bilangan-bilangan lain yang menjadi subset dari bilangan rasional.

Contohnya:

1/4 menjadi a = 1 dan b = 4

 Bilangan rasional mencakup:


a. Bilangan Bulat
Bilangan Bulat adalah semua bilangan bukan pecahan. Bilangan bulat terdiri dari bilangan nol, positif dan negatif.
Contoh : Bilangan positif 1,2,3,4,5,6,7,… ,bilangan negatif …,-7,-6,-5,-4,-3,-2,-1 dan bilangan nol “0”

b.Bilangan Asli

Bilangan Asli adalah bilangan bulat yang dimulai dari satu.
yang termasuk bilangan ini adalah : 1,2,3,4,5,6,7,8,9,…

c.Bilangan Cacah

Bilangan Cacah adalah bilangan bulat yang dimulai dari nol.
yang termasuk bilangan ini adalah : 0,1,2,3,4,5,6,7,8,9,…

 d.Bilangan Prima

Bilangan Prima adalah bilangan bulat lebih dari satu yang hanya bisa terbagi habis oleh 1 dan bilangan itu sendiri.
Contoh : Bilangan 2, 3, 5, 7, 11, 13, 17,… dll.

e.Bilangan Pecahan

Bilangan Pecahan adalah bilangan yang dinyatakan dalam bentuk  dengan “a” adalah bilangan pembilang dan “b” adalah bilangan penyebut. Dengan “b” tidak boleh sama dengan nol.

2. Bilangan Irrasional

Bilangan Irrasional

Dalam matematika, bilangan irasional adalah bilangan riil yang tidak bisa dibagi (hasil baginya tidak pernah berhenti). Dalam hal ini, bilangan irasional tidak bisa dinyatakan sebagai a/b, dengan a dan b sebagai bilangan bulat dan b tidak sama dengan nol. Jadi bilangan irasional bukan merupakan bilangan rasional. Contoh yang paling populer dari bilangan irasional adalah bilangan π, ${\displaystyle {\sqrt {2}}}$, dan bilangan e.

Bilangan π sebetulnya tidak tepat, yaitu kurang lebih 3.14, tetapi

= 3,1415926535.... atau

= 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510...

Untuk bilangan ${\displaystyle {\sqrt {2}}}$:

= 1,4142135623730950488016887242096.... atau

= 1,41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73798..

dan untuk bilangan e:

= 2,7182818....

B.Himpunan (sets)

 Segala koleksi benda-benda tertentu yang di anggap sebagai satu kesatuan atau dengan kata lain adalah kumpulan objek yang memiliki sifat yang dapat di definisikan dengan jelas.

Himpunan(sets)

General(others):

> Obyek-obyek yang membentuk suatu HIMPUNAN disebut anggota-anggota atau ANGGOTA saja.


> Obyek-obyek suatu HIMPUNAN bisa berupa orang-orang tertentu, hewan-hewan tertentu, benda-benda tertentu angka-angka tertentu dll.


> Suatu HIMPUNAN dilambangkan dengan huruf besar (A,B,C,D,E,...).


> Sedangkan ANGGOTA dilambangkan dengan huruf kecil (a,b,c,d,e,f,g,h,i,j,k,l,..).

Notasi Himpunan:

Notasi Himpunan

Simbol-Simbol Baku:

• P adalah bilangan bulat positif
• N adalah bilangan asli
• Z adalah bilangan bulat
• Q adalah bilangan rasional
• R adalah bilangan rill
• C adalah bilangan kompleks
• U adalah bilangan universal atau semesta

Penyajian Himpunan:

> Pendaftaran

   Dengan cara ini, anggota-anggota himpunan ditulis dalam kurung kurawal dan dipisahkan dengan tanda koma. Pada penulisan himpunan dengan cara mendaftar anggota-anggotanya, jika semua anggota dapat ditulis maka urutan penulisan boleh diabaikan. Jika suatu himpunan mempunyai anggota sangat banyak dan memiliki pola tertentu maka penulisannya dapat dilakukan dengan menggunakan tiga buah titik yang dibaca "dan seterusnya".

Contoh: A = {bilangan asli}, maka dapat dituliskan sebagai:

              A = {1, 2, 3, 4, . . .}.

Akan tetapi jika himpunan itu anggotanya terbatas maka kita menulisnya dengan cara:

             P = {bilangan cacah ganjil kurang dari 100}, maka:

             P = {1, 3, 5, 7, 9, . . . , 99}.      

> Pencirian

    Adapun cara lain seperti enumerasi atau tabulasi elemen-elemennya, Menggunakan simbol-simbol baku, Notasi pembentuk Himpunan,dan Diagram Venn yang sudah di jelaskan pada minggu lalu. Kali ini kita akan membahas penyajian himpunan dalam bentuk Deskriptif dan dengan menggunakan diagram seperti : diagram garis dan diagram cartess. Deskriptif yaitu menyatakan himpunan dengan menuliskan ciri-ciri umum atau sifat-sifat umum dari anggotanya.

Contoh :  D = { x │ x adalah himpunan bilangan bulat }     

                E = { x │x adalah himpunan bilangan cacah } 

                F = { x │x adalah himpunan bilangan cacah }

Hukum dan Teori Himpunan:

> Himpunan berhingga (finite set) VS himpunan tak berhingga (infinite set)

> Pencatatan anggota-anggota yang sama,di hitung sekali.

> Himpunan yang tidak mempunyai anggota disebut himpunan hampa/kosong (empty/null set) dinyatakan dengan simbol  Ø

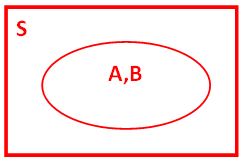
> Himpunan A dan B dikatakan sama,A=B bila mereka mempunyai ordo dan anggota-anggota yang sama.

>Dua himpunan di sebut saling lepas (saling asing/disjoint) bilatidak mempunyai anggota bersama.

                                                                                                                                                                                                                                                                                                                                                                                                                     Operasi-operasi Himpunan.

Ada beberapa operasi himpunan yang perlu diketahui, yaitu : irisan , gabungan, komplemen, selisih dan beda setangkup.

Operasi-operasi Himpunan

Irisan (intersection)

Irisan antara dua buah himpunan dinotasikan oleh tanda ‘∩ ‘.
Misalkan A dan B adalah himpunan yang tidak saling lepas, maka A ∩ B = { x | x ∈ A dan x ∈ B }
Jika dinyatakan dalam bentuk diagram Venn adalah :

irisan (intersection)

Contoh irisan :

• Misalkan A = {2, 3, 5, 7, 11} dan B = {3, 6, 9, 12}, maka A ∩ B = {3}
• Misalkan A adalah himpunan mahasiswi TI STT Telkom dan B merupakan himpunan wanita lanjut usia (50 tahun ke atas), maka A ∩ B = ∅.

Hal ini berarti A dan B adalah saling lepas atau A // B.

Gabungan (union)

Gabungan antara dua buah himpunan dinotasikan oleh tanda ‘∪‘.
Misalkan A dan B adalah himpunan, maka A ∪ B = { x | x ∈ A atau x ∈ B }

Union

Jika dinyatakan dalam bentuk diagram Venn adalah :

Contoh union :

• Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A ∪ B = { 1, 2, 3, 4, 5, 7}
• A ∪ ∅ = A

Komplemen (complement) 

Komplemen dari suatu himpunan merupakan unsur -unsur yang ada pada himpunan universal (semesta pembicaraan ) kecuali anggota himpunan tersebut. Misalkan A merupakan himpunan yang berada pada semesta pembicaraan U, maka komplemen dari himpunan A dinotasikan oleh :

Ā = { x | x ∈ U dan x ∉ A }

Jika dinyatakan dalam bentuk diagram Venn adalah :

Komplemen

Contoh komplemen :

• Misalkan U = { 1, 2, 3, ..., 9 },
• jika A = {1, 3, 7, 9}, maka Ā = {2, 4, 5, 6, 8}
• jika A = { x ∈ U | x habis dibagi dua }, maka A= { 1, 3, 5, 7, 9 }

Contoh komplemen :

A = himpunan mahasiswa STT Telkom

B = himpunan mahasiswa yang tinggal di Asrama

C = himpunan mahasiswa angkatan 2004

D = himpunan mahasiswa yang mengambil matematika diskrit

E = himpunan mahasiswa yang membawa motor untuk pergi ke kampus

a. Pernyataan

“Semua mahasiswa STT Telkom angkatan 2004 yang membawa motor untuk pergi ke kampus” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

(A ∩ C) ∩ E

b. Pernyataan

“Semua mahasiswa STT Telkom yang tinggal di asrama dan tidak mengambil matematika diskrit” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

A ∩ B ∩ D

c. Pernyataan

“semua mahasiswa angkatan 2004 yang tidak tinggal di asrama atau tidak membawa motor untuk pergi ke kampus” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

C ∩ (B ∪ E)

Selisih (difference)

Selisih antara dua buah himpunan dinotasikan oleh tanda ‘– ‘. Misalkan A dan B adalah himpunan, maka selisih A dan B dinotasikan oleh A – B = { x | x ∈ A dan x ∉ B } = A ∩ B

Selisih

Contoh selisih :

Jika A = { 1, 2, 3, ..., 10 } dan B = { 2, 3, 5, 7}, maka A – B = { 1, 4, 6, 8, 9 } dan B – A = ∅

Beda Setangkup (Symmetric Difference)

Beda setangkup antara dua buah himpunan dinotasikan oleh tanda ‘⊕‘.
Misalkan A dan B adalah himpunan, maka beda setangkup antara A dan B dinotasikan oleh :

A ⊕ B = (A ∪ B) – (A ∩ B)
             = (A – B) ∪ (B – A)

Jika dinyatakan dalam bentuk diagram Venn adalah :

Symmetric Difference

Contoh beda setangkup :
Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A ⊕ B = { 1, 4, 7 }

Beda setangkup memenuhi sifat-sifat berikut :

• A ⊕ B = B ⊕ A (hukum komutatif)
• (A ⊕ B ) ⊕ C = A ⊕ (B ⊕ C ) (hukum asosiatif)

Perkalian Kartesian (cartesian product)

Perkalian kartesian antara dua buah himpunan dinotasikan oleh tanda ‘× ‘.
Misalkan A dan B adalah himpunan, maka perkalian kartesian antara A dan B dinotasikan oleh :

A × B = {(a, b) | a ∈ A dan b ∈ B }

Contoh perkalian kartesian :

Misalkan C = {1, 2, 3}, dan D = { a, b }, maka C × D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }
Misalkan A = B = himpunan semua bilangan riil, maka A × B = himpunan semua titik di bidang datar

Misalkan ada dua himpunan dengan kardinalitas berhingga, maka kardinalitas himpunan hasil dari suatu perkalian kartesian antara dua himpunan tersebut adalah perkalian antara kardinalitas masing-masing himpunan. Dengan demikian, jika A dan B merupakan himpunan berhingga, maka:

|A × B| = |A| . |B|

Pasangan terurut (a, b) berbeda dengan (b, a), dengan kata lain (a, b) ≠ (b, a). Dengan argumen ini berarti perkalian kartesian tidak komutatif, yaitu

A × B ≠ B × A

dimana A atau B bukan himpunan kosong. Jika A = ∅ atau B = ∅, maka

A × B = B × A = ∅

SEMOGA BERMANFAAT