Matriks Dasar
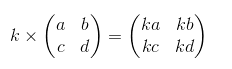
Contoh:
d. Perkalian Matriks dengan Matriks
Seperti yang telah disinggung sebelumnya ya guyss, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.
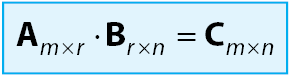
Sebelum
mengulas cara melakukan operasi perkalian dua buah matriks, sebaiknya
kita perlajari dahulu sidat-sifat operasi perkalian dua matriks guyss.
Sifat-sifat operasi perkalian matriks meliputi sifat asosiatif,
distributif, dan memiliki matriks identitas I. Sifat-sifat operasi
perkalian matriks dapat dilihat pada gambar di bawah.

Berikut contoh soalnya guyss:
Berdasarkan ordo Matriks dapat di bagi menjadi beberapa jenis yaitu :
Gimana? Sudah paham belum? kalau belum ulangi lagi yaaaa, pahami baik-baik. Mungkin cukup sekian materi yang bisa saya berikan, semoga bisa dipahami yaaaaa. See you in the next blog^^^
 | ||
| Matriks |
Hallooooooooo guysss .... apa kabar nihhh? Semoga baik-baik aja yahhh :).Jadi ceritanya kali
ini gw akan akan ngebahas nihh tentang “apa itu MATRIKS?”. Materi
matriks ini kita jumpa di kelas 1 SMA bukan guysss, masih ingat kan? Yuk langsung ajaaa kita masuk ke materi nihhh,come on !!!
Teori Dasar Matriks
Hayooo ngomong-ngomong ada yang tau belum nih tentang pengertian matriks????
Matriks ituuu merupakan sekumpulan bilangan yang disusun secara baris dan kolom yang
ditempatkan didalam suatu kurung gaesss.Atau bisa juga nihh disebut sebagai sekumpulan angka-angka, unsur-unsur ,
elemen-elemen, yang disusun berdasarkan baris dan kolom yang dibatasi
dengan tanda [ ] ( kurung siku ).
Guysss dalam penamaan/notasi matriks harus menggunakan huruf kapital yaa, sedangkan
elemen-elemen di dalamnya dinotasikan dengan huruf kecil sesuai dengan
penamaan matriks dan diberi indeks ij. Indeks tersebut menyatakan posisi
elemen matriks, yaitu pada baris i dan kolom j. jangan sampai ga tau ya?
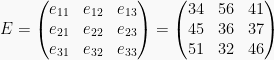 Dimana,
Dimana,  adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom
ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya. Seterusnya
seperti itu sampai pada akhir berapa banyak baris dan kolom yang
terdapat pada matriks tersebut yang biasa disebut dengan Ordo.
adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom
ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya. Seterusnya
seperti itu sampai pada akhir berapa banyak baris dan kolom yang
terdapat pada matriks tersebut yang biasa disebut dengan Ordo.
a. Penjumlahan Matriks
Syaratnya harus memiliki ordo yang sama ya guyss, dan menambahkan pada posisi atau letak yang sama.
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Jadi kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama guys.
Contoh:
b. Pengurangan Matriks
Sama seperti pada penjumlahan matriks ya guyss, pengurangan matriks hanya dapat dilakukan pada matriks-matriks yang mempunyai ukuran yang sama. Jika ukurannya berbeda maka matriks hasil tidak terdefinisikan.
Contoh :
Matriks A memiliki ordo 2x2. Kemudian matriks B memiliki ordo 2x3,
matriks C memiliki ordo 3x1, matriks D memiliki ordo 1x2, serta matriks E
memiliki ordo 1x1.
Operasi Matriks
guysss tau ngga operasi matriks itu gimana? nih bakal dibahas guyss kuyyyy......
a. Penjumlahan Matriks
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Jadi kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama guys.
Contoh:
b. Pengurangan Matriks
Sama seperti pada penjumlahan matriks ya guyss, pengurangan matriks hanya dapat dilakukan pada matriks-matriks yang mempunyai ukuran yang sama. Jika ukurannya berbeda maka matriks hasil tidak terdefinisikan.
c. Perkalian Matriks dengan Skalar
Sedangkan untuk penjelasan dari perkalian skalar matriks dilakukan dengan cara konstanta yang artinya
nilai matriks bisa dikalikan dengan cara mengalikan setiap eleman atau komponen nilai matriks dengan skalar. Misalnya nilai Matriks A dikalikan dengan skalar K maka setiap eleman atau komponen Matriks A dikali dengan k.
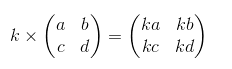
Contoh:
d. Perkalian Matriks dengan Matriks
Seperti yang telah disinggung sebelumnya ya guyss, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.
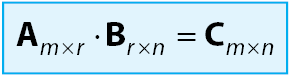

Berikut contoh soalnya guyss:
Jenis-jenis Matriks
- Matriks Bujursangkar adalah matriks yang memiliki ordo n x n atau banyaknya baris sama dengan banyaknya kolom yang terdapat dalam mtriks tersebut. Matriks ini disebut juga dengan matriks persegi berordo n.
Contoh :
- Matriks Baris adalah Matriks Baris adalah matriks yang terdiri dari satu baris
Contoh : A = ( 2 1 3 -7 )
- Matriks Kolom adalah Matriks Kolom adalah matriks yang terdiri dari satu kolom.
Contoh :
- Matriks Tegak adalah suatu matriks yang banyaknya baris lebih dari banyaknya kolom.
Contoh :
- Matriks datar adalah Matriks yang banyaknya baris kurang dari banyaknya kolom.
Contoh :
Berdasarkan elemen-elemen penyusunnya matriks dapat di bagi menjadi beberapa jenis yaitu :
- Matriks Nol adalah Suatu matriks yang setiap unsurnya 0 berordo m x n, ditulis dengan huruf O.
- Matriks Diagonal adalah suatu matriks bujur sangkar yang semua unsurnya , kecuali unsur-unsur pada diagonal utama adalah nol.
- Matriks Segi Tiga adalah suatu matriks bujur sangkar yang unsur-unsur dibawah atau diatas diagonal utama semuanya 0 .
Dimana Matriks C disebut matriks segi tiga bawah dan matriks D disebut matriks segitiga atas.
- Matriks Skalar adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya sama.
- Matriks Identitas atau Matriks Satuan adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya satu ditulis dengan huruf I.
- Matriks Transpos ( notasi At )
Gimana? Sudah paham belum? kalau belum ulangi lagi yaaaa, pahami baik-baik. Mungkin cukup sekian materi yang bisa saya berikan, semoga bisa dipahami yaaaaa. See you in the next blog^^^



















Komentar
Posting Komentar